Optimizing Public WNFS Divergence Search

[Quinn]

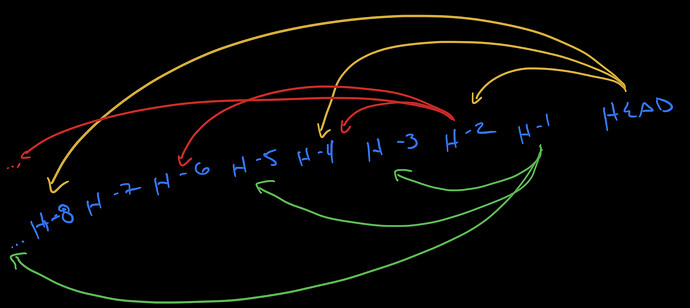
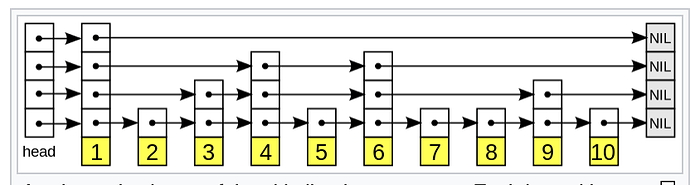
Background

Imagine that an agent comes online, and learns that the latest remote revision of a public WNFS tree is different from the local revision. This means one of three things:

1. The local tree is an ancestor of the remote tree (i.e. the remote is strictly newer)
   • Fast forward the local tree to point at the remote revision
2. The remote tree is an ancestor of the local tree (i.e. the remote is strictly older)
   • Nothing needs to be done to the local tree
3. Both trees have diverged (but share a common ancestor)
   • Run the reconciliation algorithm (i.e. choose the revision with the lowest hash)

In order to determine which case we’re looking at, the lowest common ancestor of both trees must be found. This is a process that can take some time, and may be worth optimizing.

Current Approach

As I understand it, the current approach is to walk backwards through the history for both trees, until you find a common node. Since this traversal happens one revision at a time, if two trees have diverged over many updates, it may require many round trips in order to locate this ancestor.

Proposed Alternatives

1. Skip List

I’m not super familiar with the specifics of this proposal, and I believe it’s mostly @expede and @matheus23’s idea, but the high-level concept is to overlay a deterministic skip list onto the history, to be used in traversing the history in variable sized jumps.

There’s lots more to be said about this approach, but I don’t want to misrepresent the idea, since it was only briefly conveyed to me during my onboarding call with @expede. Feel free to edit with more information!

2. Consistent Contraction Hierarchy (Consistent Skip List?)

This idea combines two different concepts: hash partitioning (sometimes called consistent hashing), and contraction hierarchies.

Hash Partitioning

Hash partitioning is an algorithm that’s typically used for distributing a value among a number of possible buckets, in a distributed fashion, with minimal coordination.

In its simplest case, it works by partitioning the output of a hash function into n buckets, and then hashing a given value: the resulting hash will map to one of those n buckets. Since every client will compute the same bucket for the same values, this is sometimes used in distributed databases, as a technique for choosing which shard of a cluster the data should be stored on.

From “Designing Data-Intensive Applications”:

We’ll get back to this idea after discussing contraction hierarchies.

Contraction Hierarchies

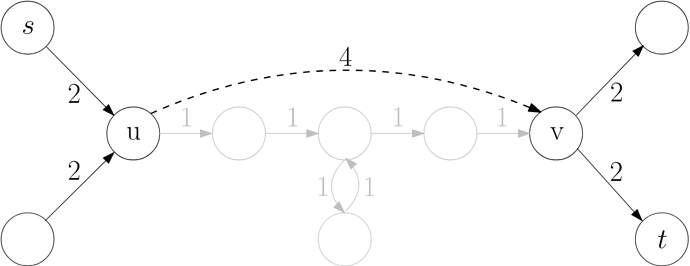
Contraction hierarchies can be used to speed up the process of finding the shortest path in a graph. The idea is to associate a graph with a simpler “contraction” of that graph, such that rather than searching the original graph, you can simply search the contraction and then map the discovered path back to the original graph in order to prune the search space.

In the below example, pre-computing the shortest path between u and v means that finding the shortest path from s and t can simply reuse that path as a “shortcut”.

This shows up in navigation systems. For example, if I want to find the shortest path from the University of Waterloo to the University of Toronto, and every intersection in the country is stored in a graph, it doesn’t make sense to search every possible path between both endpoints. Instead, a simpler “contraction” can be precomputed, that stores the shortest path between every city in the country.

Now, the problem has been reduced to finding the shortest path from the University of Waterloo to the perimeter of Waterloo, and from the perimeter of Toronto to the University of Toronto: everything in between can use the precomputed path linking the two cities. Further optimizations can be achieved by layering on multiple granularities of contractions on top of each other.

In the case of a graph that describes the roads in a country, its obvious how to contract the graph to achieve this sort of nesting: you use stable and meaningful geographic markers like “post offices”, “major intersections”, or “highway on-ramps”. But how do you achieve the same thing in the abstract world of content-addressable filesystems?

Combining the Two

To me, our fundamental problem is one of choosing consistent breakpoints in the history, in a distributed fashion, such that they can be used to select the nodes that belong to a given contraction. If we can achieve that, then we can construct contraction hierarchies over the revision history for a WNFS filesystem, that map to approximate indices into that history, and we can use those as checkpoints when searching for a least common ancestor.

While hash partitioning is typically used for partitioning space into a number of buckets, I think we can use the same idea to partition time in a similar way. The general approach I have in mind is to use the hashes of the CIDs within a revision history to bucket those revisions into different levels of the hierarchy, such that neighboring revisions within a given contraction represent predictable and consistent jumps through the history.

One way to do this is to steal Bitcoin’s idea of a hash target. Since CIDs are uniformly distributed, we can define a target “width”, w, for each level of the hierarchy, and choose a hash target for that level such that we’re expected to a find a CID below that target every w revisions. By arranging these targets end to end into non-overlapping intervals, we partition the CID-space into a contraction hierarchy that matches our desired properties!

The choice of hash target essentially maps to the birthday problem. In our case, the width of a contraction gives the number of people required for a 50% chance of hitting our target, and we’re solving for the number of “days”, D, such that hash_target = 2**32/D. Calculators for the birthday problem exist, and a particularly nice one can be found here.

Now, when adding new revisions to IPFS, in addition to back-pointers to the previous revision, they can also include pointers to the previous revisions under each level of the contraction hierarchy! Let’s call these “checkpoint” revisions.

Since the hierarchies are consistently constructed regardless of reference point, this means that finding the least common ancestor of two nodes reduces to walking backwards along the largest contraction in the hierarchy until a common checkpoint is found.

The process can then be repeated for each smaller contraction, beginning with the predecessor of the shared ancestor for the previous contraction, until the least common ancestor has been found. This allows us to move along the revision history in massive leaps, while guaranteeing that we eventually find the common ancestor.

Consider this example:

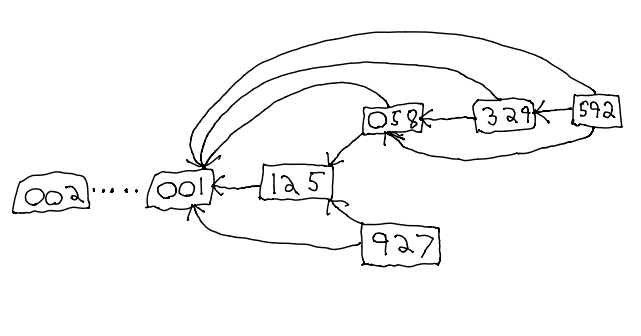
Here we have a contraction hierarchy made up of two contractions, plus the per-revision linked list we have now. Each contraction is computed based on the number of zeros at the beginning of the hash: the widest contraction is made up of the nodes with two leading zeroes, and next with nodes having one leading zero.

If we want to find the least common ancestor of nodes 592 and 927, we start by comparing the pointers for the widest contraction: since both point to 001, we know that the least common ancestor appears after 001. Now we follow the pointers for the next level of contraction, and end up at 125 and 058. Since both share ancestors under this level of transaction, we consider the linked list of revisions, and immediately see that 058 links to 125, which must be the least common ancestor for 592 and 927.

For this example, the hashes are made up, and the points don’t matter, but this whole search happens using 2 round-trips (fetching 125 and 058), versus 3 with only a linked list (329, 058, 125).

In a sense, because the hash function partitions the timeline into intervals, with some consistent checkpoint as their start-point, we’re always able to find our position relative to absolute checkpoints into that history, even if we’re not aware of our precise index through the timeline. This anchors the search to these checkpoints and prunes out everything else. I don’t think it would be inaccurate to say that the resulting structure mirrors that of a skip list, where relative links are replaced with absolute links.

Implementation Details

The above is a high-level sketch of the idea, but there still exist a few implementation details to be worked out:

1. How large should the contraction hierarchy be?
   • Less contractions ⇒ less time-efficient to search within the interval given by the widest contraction
   • More contractions ⇒ less space-efficient to store the links within that interval
2. What should the width of each contraction be?
   • Wider contractions ⇒ more contractions required to efficiently navigate the interval give by that contraction
   • Narrower contractions ⇒ fewer contractions required to efficiently navigate that interval
3. How many back-pointers should each node store for each contraction?
   • Rather than traversing backward one pointer at a time, we can store pointers to the last k nodes for each contraction
   • Reduces the round trips needed to find the common ancestor for each contraction
   • Increases the storage costs of each node
4. Should the pointers to the last node in the contraction be stored in IPFS, or constructed locally?
   • Storing them remotely allows them to be reused by multiple clients
   • Perhaps it’s uncommon for multiple clients to be working off the same divergent branch of history? If most clients work off their own branch, then this work may not be reused anyway
   • Can instead track them locally, as revisions are added
   • Possible middle-ground: checkpoint nodes store pointers to other checkpoints, but most revisions do not?
     • Once a checkpoint has been found, you can quickly navigate the history, but avoid storing these pointers on other nodes, and instead cache them in memory

Conclusion

I have no idea how often this problem ends up being a bottleneck in practice, or whether it’s worth spending too much time exploring an optimization to what’s already there, but an approach like those described above may go a long way toward speeding up pathological cases to do with merging public WNFS trees.

I’m personally a fan of the contraction hierarchy approach: the way it partitions the timeline into roughly fixed-width intervals that we can reason about independently seems like a powerful abstraction for reducing this problem in cases where timelines have diverged over hundreds or thousands of revisions.

That being said, I recognize that I’m biased here, and also that I haven’t given the skip list approach as detailed of a treatment, so I invite anyone with a clearer idea of the skip list proposal to flesh that section out with more details if they think there’s more worth exploring there!

Anyway, my larger goal was just to document these thoughts!

[expede]

Thanks for writing this up @Quinn

The short version is that I’m pretty sold on the hash target to get a that “highway” where we only look at every (average) n elements. There’s some detail here on how we want to get to the highway on-ramp, but in general I think that this is a very attratcive method

1. Easy to find a common node, improvement of the initial search phase by some constant factor
2. Uses the existing CIDs
3. Doesn’t preclude us from adding a skip list later if we also want that for some reason

At this point, I think this is pretty much a slam dunk We should figure out the exact skip weights, and design the exact details of reconciliation search

[expede]

@Quinn

1. Skip List

I’m not super familiar with the specifics of this proposal, and I believe it’s mostly @expede and @matheus23’s idea, but the high-level concept is to overlay a deterministic skip list onto the history, to be used in traversing the history in variable sized jumps.

There’s lots more to be said about this approach, but I don’t want to misrepresent the idea, since it was only briefly conveyed to me during my onboarding call with @expede. Feel free to edit with more information!

The idea is essentially that we can maintain n links to get a constant-factor speedup (actually it’s O(log n) at the limit) on the number of nodes that have been seen. This works under the assumption that you don’t know a common node (turns out that we can get this with hash targets), so you’re searching for a relative value relative to the each head.

This looks something like this:

So, at HEAD, we explore n (in this case 4, in powers of 2) CIDs. Every node that we explore backwards shows us up to another n. This gives us lots of possibilities for exploring the space in parallel, as we can search really far back in time, and do classic exponential split search strategies, and so on. We know the exact relative index from head even if we do multiple large jumps back, so it’s easy to build a table and know which one is where in the list.

Why the Hash Target is Better

We’re looking for a common node and this gives us an easy way to find nodes in common, not based on numbering. I started calling this the “search highway”, because we can make it some semi-large number, so we can get a “which order or magnitude?” search scope.

This is also self-verifying. We can pick whatever hash criterion, and it’s self-evident from the content. Maliciously creating hashes to make the search space O(n) is equivalent to PoW, so possible but also takes a lot of hash power for the attacker.

The more credible attack is omitting links or skipping values when creating new nodes. If they skip nodes, we need to perform an O(n) search inside that interval, but that’s where we’re at today Also as long as they don’t use the genesis node, we still get both some shrinking of the search space, and knowledge of if there are any shared nodes.

Probabilistic Skip Lists

This is actually not that different from a probabilistic skip list. These depend on randomness to decide if you should put a link to that specific node. A lot of cryptographic protocols upgrade to being noninteractive by using hashing as a replacement for coin flips, to make all clients agree, do fewer round trips (i.e. exactly one in the case on noninteractivity), and so on.

We can do apply this hash target technique to do multiple “levels”, just like a skip list. It doesn’t let users know how quickly they’re searching back in time (maybe still useful to have a deterministic skip list?), but does make it really easy to build and validate.

(Multilevel skip list)

[Quinn]

@expede

This is actually not that different from a probabilistic skip list.

I missed this connection, but you’re totally right! I really like that framing of the data structure.

[expede]

@expede

There’s some detail here on how we want to get to the highway on-ramp, but in general I think that this is a very attratcive method

e.g. does every node maintain a pointer to the last on-ramp? Do we use smaller hops to get there sooner? If so, based on different harness criteria, they accidentally skip over a highway, so they need to be designed together? Do we run a linear search until we hit the highway? Lots of options here, all with their own tradeoffs!

[matheus23]

One thing I want to highlight that I think we should keep in mind:
With any version of these link-skipping optimizations, we’ll always have a “source-of-truth” problem: What happens if a malicious or buggy client creates a WNFS that contains incorrect skip links?
The source of truth must always be the single-revision-jumping previous links, since only they contain all information about the WNFS revisions.

If the skip links aren’t the source-of-truth this means that we have to walk the previous links anyway to verify that the skip links are correct, possibly destroying any performance gain.
What we can do is run two computations in parallel: One computation assumes the skip links are correct and already jumps ahead and performs the WNFS merge, while the other computation tries to verify the skip links concurrently.

Another problem is how to handle broken invariants once they got into the system. Let’s say a buggy client now successfully wrote incorrect skip links to WNFS and our server didn’t check them yet/is also buggy/it didn’t go through our server, but was gossiped peer-to-peer.
Once a non-buggy client detects these skip links, does keep these revisions and just “does it correctly” from then on, building on the incorrect revisions?
Or does it ignore these revisions and continues from the oldest known correct state?
Or does it try to “migrate” these incorrect filesystem blocks and fix all the skip links?
If this ends up happening, we have some version of a “distributed migration problem”.

A way to mitigate that is to split out the “duplicate” information (skip links) from the integrity check of the public tree (i.e. WNFS public root hash).
Concretely that means that we’re not storing the skip links in WNFS blocks directly, but outside. For some optimizations that might mean each client only trusts itself with building indexes.
However, for skip links the actual gain comes from gossiping them around. One way this could work would be another entry in the root WNFS directory, but outside of the public/ subtree.

Also I should note that we should definitely also weigh all of the above against what we think the likelihood of these concerns actually happening are, how much damage they would cause and how high the implementation cost of applying a mitigation would be.

[expede]

Totally, yeah. One of the things that I like about the hash target version is that we can validate it in constant time. This doesn’t mean that it’s the next one, just that it’s on a “highway”. An attacker can create a parallel tree, and send you down it if you use the highway, which is not great… but purely for reconciliation (not a user searching history), we’d still get a common node, or run out of history. The purpose is to shrink our search history, where the worst case scenario (no common highway nodes) puts us where we’re at today.

[Quinn]

@matheus23

With any version of these link-skipping optimizations, we’ll always have a “source-of-truth” problem: What happens if a malicious or buggy client creates a WNFS that contains incorrect skip links?

These are really great questions to be asking!

I have two responses to this, but they rely on implementation details of WNFS I’m less familiar with than you, so please correct me if I’m wrong

First, as Brooke mentioned above, about the hash targets:

@expede

This is also self-verifying. We can pick whatever hash criterion, and it’s self-evident from the content. Maliciously creating hashes to make the search space O(n) is equivalent to PoW, so possible but also takes a lot of hash power for the attacker.

While it is possible for an attacker to forge hash links, doing so requires that they’re able to construct as many revisions as it would take to end up with a “checkpoint” naturally. Because of this, I don’t believe there’s any new risk of them launching a new denial of service on the system, since any checkpoints they link to will still be ancestors in the history.

Those checkpoints may skip over other checkpoints, but that case is already handled by the LCA (least common ancestor) algorithm: if at any point a common ancestor for the narrowest contraction level isn’t found, then we fall back to traversing the links one-by-one. It’s a pathological case that an attacker can induce, but I believe it’s one with roughly the same runtime characteristics as the current system.

Second, the risk of hiding nodes like this also applies to forged “last revision” pointers: there’s nothing stopping an attacker from forging a new history entirely, to force walking across an entirely bifurcated history. BUT! Since all histories eventually lead to the same root tree, this can be detected through the same process we’d go through when merging two valid and long-diverged histories.

One risk we haven’t written about though, is that this sort of forgery allows an attacker to “hide” a filesystem revision. It can still be found by walking through all of the DAGs, but it will be less likely to surface during an efficient traversal of the history. Brooklyn brought up that this might pose concerns around hiding CSAM in the history, and that’s a threat model worth thinking about, but I believe it’s orthogonal to the design choices we’re talking about here.

These are really important things to be thinking about though, and I’m glad you bring them up, because I should have addressed these in the original post!

[expede]

@matheus23

With any version of these link-skipping optimizations, we’ll always have a “source-of-truth” problem

Sorry, I should probably highlight that you are in fact correct. This was the big snag for the skip list version, which caused us a bunch of grief. There’s this super tricky balance between “can’t go wrong” (in the correct-by-construction sense), wanting performance gains, and attack surface.

Turns out this is hard

[matheus23]

What are your thoughts on the idea of putting these skip links next to the public filesystem (sort of like an index) instead of inside of it?
This way we’re decoupling the correctness of the skip links/index from the public tree itself, more concretely: We can throw away the index and recreate it if we figure out something went wrong without having to change the public filesystem. I think this is a huge advantage since this makes changing the index/skip list for any reason (maybe we come up with a better structure in the future?) much cheaper: We want the hashes of blocks in the public filesystem to be as long-lived as possible, since they’re used to witness causal relationship.

[matheus23]

Oh and should we perhaps move this into a discussion at https://github.com/WebNativeFileSystem/spec to loop in Brendan & Kasey?

[Quinn]

Thanks Philipp, that’s a good idea! I’ve opened up an issue for discussion in the spec repo: https://github.com/WebNativeFileSystem/spec/issues/1